Back
Purpose: Prediction of the tensile strength of compacted mixtures from pure components is of great practical importance. As a result, Ryshkewitch-Duckworth (RD) based models have been proposed in the literature. These models are presented in Table 1. The literature contains conflicting conclusions about their applicability. Thus, it is important to understand when these models produce the most divergent predictions based on the same input information. Secondly, it is crucial to identify whether a specific model is generally more accurate than the others. This study aimed to a) evaluate the effect of input parameters of pure components on differences between different models and b) identify the most accurate model among the RD-based models.
Methods: All 4 models depend on the RD intercepts (σ0) and slopes (k) of pure components. Thus, we examined the difference between the models as a function of the relative magnitude of these parameters. Eleven pure components with widely varied RD parameters and compression behaviors were collected from literature studies (1-5). The 11 components gave 55 binary combinations. The relative differences between the models’ predicted tensile strengths were determined by calculating the ratio of strength predicted by different models. The effect of the RD parameters of pure components on the difference between the models was evaluated. To identify the most accurate model, a combined set of mixture tensile strength measurements from the literature was used to compare the relative accuracy of each model. The compactibility profiles of individual components and binary mixtures were collected from five literature reports (1-5). The volume fraction of each component was calculated from their weight fraction and true density. The tensile strengths and volume fractions of the components were used to predict the tensile strength of compacted mixtures using the different models. Root Mean Square Error (RMSE) was used to assess the accuracy of each model.
Results: The differences between models as a function of the relative magnitude of RD parameters are shown in Figure 1. The differences between a given pair of models were found to be correlated to either of the RD parameters. The accuracies of the models in predicting the tensile strengths of the binary mixtures from the current set of literature data are summarized in Table 2. The correlations observed in Figure 1 can be used to explain the relative performances of given pair of models in predicting mixtures from Table 2. For instance, the difference between models 1 and 2 was strongly correlated to the ratio of σ0 of pure components (Figure 1a). The difference increased with an increase in the ratio of σ0. This implies that at lower ratios, the strength predictions by these models were nearly equal. This finding was consistent with the approximately similar performance of both models in predicting mixtures from studies: Eftaiha et al., Tye et al., and Wu et al., where components displayed ratios of ≤2.5 for σ0. At higher ratios, the predictions generated by these models were distinct. This can be exemplified by binary mixtures from Patel & Bansal, where components displayed ratios ≥15.8 for σ0. In this study, model 2 showed higher RMSE than model 1. Similar conclusions can be drawn for the other comparisons shown in Figure 1, where % differences between models were directly correlated to the ratio of either of the RD parameters. All models depend on the RD parameters of pure components. Thus, the similarities/differences in the performance of different models in predicting specific binary mixtures can be explained by accounting for the effect of the ratio of RD parameters of mixture components. Overall, model 1 was the most accurate, with an overall RMSE of 0.25 MPa for the complied dataset. For individual mixtures, model 1 was the most accurate in all but 2 mixtures. Even when model 1 was not the most accurate prediction of an individual mixture’s strength, the RMSE for the model was only 0.03 and 0.11 MPa larger than the most accurate model.
Conclusion: All RD-based models have shown usefulness in predicting specific binary mixtures, although most are not generally applicable to accurately describe the behavior of more diverse mixtures. Based on the analysis of 10 binary mixtures from five previously published studies, it can be concluded that model 1 is the most accurate RD-based model. The other models have shown applicability primarily only when they approximate model 1. Although model 1 performed better than others, caution should be exercised as the RMSE was as high as ~0.4 MPa in certain mixtures.
References: 1. Patel & Bansal, 2011. Int. J. Pharm., 403(1-2), 109-114.
2. Eftaiha et al., 2009. J. Mater. Sci., 44, 1054-1062.
3. Tye et al., 2005. J. Pharm. Sci., 94(3), 465-472.
4. Wu et al., 2005. Eur. J. Pharm. Sci., 25(2-3), 331-336.
5. Etzler et al., 2011. J. Adhes. Sci. Technol., 25(4-5), 501-519.
.jpg) Table 1. Models based on the application of the Power Law (P) and Linear Mixing Rule (L) to the Ryshkewitch-Duckworth (RD) Equation.
Table 1. Models based on the application of the Power Law (P) and Linear Mixing Rule (L) to the Ryshkewitch-Duckworth (RD) Equation.
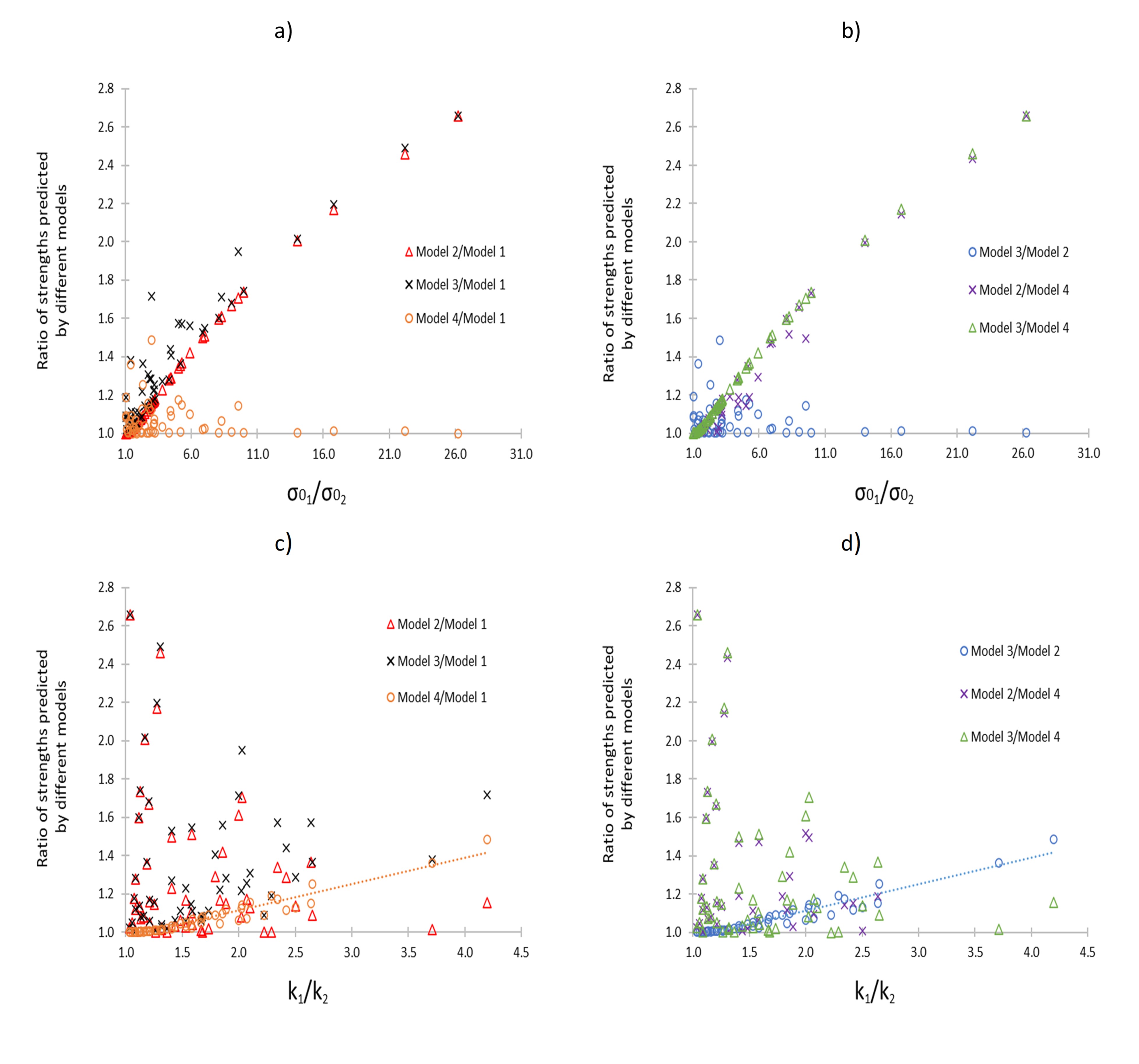 Figure 1. The differences in strength predictions between different models as a function of RD parameters; (a & b) σ0 and (c & d) k of pure components. The analysis was performed at a porosity of 0.15 for a 1:1 mixture composition. Similar trends were also observed at different porosities and mixture compositions.
Figure 1. The differences in strength predictions between different models as a function of RD parameters; (a & b) σ0 and (c & d) k of pure components. The analysis was performed at a porosity of 0.15 for a 1:1 mixture composition. Similar trends were also observed at different porosities and mixture compositions.
.jpg) Table 2. The prediction performance of different models
Table 2. The prediction performance of different models
Formulation and Delivery - Chemical
Category: Late Breaking Poster Abstract
(T1230-03-21) Applicability of Ryshkewitch-Duckworth Based Models to Predict the Tensile Strength of Compacted Mixtures
Tuesday, October 24, 2023
12:30 PM – 1:30 PM ET
- PV
Pradeep Valekar, M.S. (he/him/his)
Graduate student
Duquesne University
Pittsburgh, Pennsylvania, United States - PV
Pradeep Valekar, M.S. (he/him/his)
Graduate student
Duquesne University
Pittsburgh, Pennsylvania, United States - IB
Ira S. Buckner, Ph.D. (he/him/his)
Duquesne University
Pittsburgh, Pennsylvania, United States
Presenting Author(s)
Main Author(s)
Co-Author(s)
Purpose: Prediction of the tensile strength of compacted mixtures from pure components is of great practical importance. As a result, Ryshkewitch-Duckworth (RD) based models have been proposed in the literature. These models are presented in Table 1. The literature contains conflicting conclusions about their applicability. Thus, it is important to understand when these models produce the most divergent predictions based on the same input information. Secondly, it is crucial to identify whether a specific model is generally more accurate than the others. This study aimed to a) evaluate the effect of input parameters of pure components on differences between different models and b) identify the most accurate model among the RD-based models.
Methods: All 4 models depend on the RD intercepts (σ0) and slopes (k) of pure components. Thus, we examined the difference between the models as a function of the relative magnitude of these parameters. Eleven pure components with widely varied RD parameters and compression behaviors were collected from literature studies (1-5). The 11 components gave 55 binary combinations. The relative differences between the models’ predicted tensile strengths were determined by calculating the ratio of strength predicted by different models. The effect of the RD parameters of pure components on the difference between the models was evaluated. To identify the most accurate model, a combined set of mixture tensile strength measurements from the literature was used to compare the relative accuracy of each model. The compactibility profiles of individual components and binary mixtures were collected from five literature reports (1-5). The volume fraction of each component was calculated from their weight fraction and true density. The tensile strengths and volume fractions of the components were used to predict the tensile strength of compacted mixtures using the different models. Root Mean Square Error (RMSE) was used to assess the accuracy of each model.
Results: The differences between models as a function of the relative magnitude of RD parameters are shown in Figure 1. The differences between a given pair of models were found to be correlated to either of the RD parameters. The accuracies of the models in predicting the tensile strengths of the binary mixtures from the current set of literature data are summarized in Table 2. The correlations observed in Figure 1 can be used to explain the relative performances of given pair of models in predicting mixtures from Table 2. For instance, the difference between models 1 and 2 was strongly correlated to the ratio of σ0 of pure components (Figure 1a). The difference increased with an increase in the ratio of σ0. This implies that at lower ratios, the strength predictions by these models were nearly equal. This finding was consistent with the approximately similar performance of both models in predicting mixtures from studies: Eftaiha et al., Tye et al., and Wu et al., where components displayed ratios of ≤2.5 for σ0. At higher ratios, the predictions generated by these models were distinct. This can be exemplified by binary mixtures from Patel & Bansal, where components displayed ratios ≥15.8 for σ0. In this study, model 2 showed higher RMSE than model 1. Similar conclusions can be drawn for the other comparisons shown in Figure 1, where % differences between models were directly correlated to the ratio of either of the RD parameters. All models depend on the RD parameters of pure components. Thus, the similarities/differences in the performance of different models in predicting specific binary mixtures can be explained by accounting for the effect of the ratio of RD parameters of mixture components. Overall, model 1 was the most accurate, with an overall RMSE of 0.25 MPa for the complied dataset. For individual mixtures, model 1 was the most accurate in all but 2 mixtures. Even when model 1 was not the most accurate prediction of an individual mixture’s strength, the RMSE for the model was only 0.03 and 0.11 MPa larger than the most accurate model.
Conclusion: All RD-based models have shown usefulness in predicting specific binary mixtures, although most are not generally applicable to accurately describe the behavior of more diverse mixtures. Based on the analysis of 10 binary mixtures from five previously published studies, it can be concluded that model 1 is the most accurate RD-based model. The other models have shown applicability primarily only when they approximate model 1. Although model 1 performed better than others, caution should be exercised as the RMSE was as high as ~0.4 MPa in certain mixtures.
References: 1. Patel & Bansal, 2011. Int. J. Pharm., 403(1-2), 109-114.
2. Eftaiha et al., 2009. J. Mater. Sci., 44, 1054-1062.
3. Tye et al., 2005. J. Pharm. Sci., 94(3), 465-472.
4. Wu et al., 2005. Eur. J. Pharm. Sci., 25(2-3), 331-336.
5. Etzler et al., 2011. J. Adhes. Sci. Technol., 25(4-5), 501-519.
.jpg) Table 1. Models based on the application of the Power Law (P) and Linear Mixing Rule (L) to the Ryshkewitch-Duckworth (RD) Equation.
Table 1. Models based on the application of the Power Law (P) and Linear Mixing Rule (L) to the Ryshkewitch-Duckworth (RD) Equation. Figure 1. The differences in strength predictions between different models as a function of RD parameters; (a & b) σ0 and (c & d) k of pure components. The analysis was performed at a porosity of 0.15 for a 1:1 mixture composition. Similar trends were also observed at different porosities and mixture compositions.
Figure 1. The differences in strength predictions between different models as a function of RD parameters; (a & b) σ0 and (c & d) k of pure components. The analysis was performed at a porosity of 0.15 for a 1:1 mixture composition. Similar trends were also observed at different porosities and mixture compositions. .jpg) Table 2. The prediction performance of different models
Table 2. The prediction performance of different models